IFT-2002
Informatique Théorique
H14 - cours 5
Julien Marcil - julien.marcil@ift.ulaval.ca
Cours précédents
Grammaire
Une grammaire consiste en un ensemble fini de règles de réécriture (ou règles de productions ou règles de substitution).
$$ \begin{align} S \rightarrow & 0S1 \\ S \rightarrow & B \\ B \rightarrow & \lambda \end{align} $$
Dérivation
Une grammaire génère une séquence par dérivation.
$$ \begin{align} S ⇒ & 0S1 \\ ⇒ & 00S11 \\ ⇒ & 000S111 \\ ⇒ & 000B111 \\ ⇒ & 000\lambda111 \\ ⇒ & 000111 \end{align} $$
Grammaire
Définition: Une grammaire consiste en un quadruplet de la forme $(V, \Sigma, S, R)$ où
- $V$ est ensemble fini de variables (symboles non terminaux).
- $\Sigma$ est l’alphabet (symboles terminaux).
- $S \in V$ est le symbole de départ.
- $R$ est un ensemble fini de règles de réécriture.
Règles de réécriture
Ces règles sont formées d’un terme de gauche, d’une flèche ($\rightarrow$) et d’un terme de droite.
Les termes gauche et droit peuvent être n’importe quelle combinaison de symboles de $V$ ou de $\Sigma$, pourvu qu’il y ait au moins un symbole de $V$ à gauche. Le côté droit peut être vide, ce qui est indiqué par un $\lambda$.
Conventions
- Les majuscules sont des symboles non terminaux.
- Les minuscules sont des symboles terminaux.
- $S$ est le symbole initial.
Cette convention permet de simplifier la description d’une grammaire en donnant seulement la description de $R$.
Notation
$$ \begin{align} S & \rightarrow ASC & S & \rightarrow B \\ B & \rightarrow bB & B & \rightarrow \lambda \\ A & \rightarrow a & C & \rightarrow c \ \end{align} $$
Il est possible de noté les règles de réécriture plus simplement
$$ \begin{align} S & \rightarrow ASC \mid B \\ B & \rightarrow bB \mid \lambda \\ A & \rightarrow a \\ C & \rightarrow c \ \end{align} $$
Production
On nomme production l'application d'une régle de de réécriture à une chaîne de symboles terminaux et non terminaux.
Soit $u, v, w \in (V \cup \Sigma)^*$, et la régle de de réécriture $A \rightarrow w$. On dit que $uAv$ produit $uwv$, noté
$$uAv \Rightarrow uwv$$
Dérivation
On nomme dérivation l'application d'une ou plusieurs régles de de réécriture à une chaîne de symboles terminaux et non terminaux.
Soit $u, v \in (V \cup \Sigma)^*$ on dit $u$ dérive $v$, noté $$ u \overset{*}{\Rightarrow} v $$
si $u = v$ ou s'il existe $u_1,u_2,...,u_k$ pour $k \ge 0$ et
$$u⇒u1 ⇒u2 ⇒...⇒uk ⇒v$$
Langage généré par $G$
Soit la gramaire $G = (V, \Sigma, S, R)$.
$$L(G) = \{ w \in Σ^* \mid S \overset{*}{\Rightarrow} w \}$$
On dit que $L(G)$ est le langage généré par $G$.
Aujourd'hui
- Grammaire
- régulière
- hors context
- Automate à pile
Grammaire
Grammaire régulière
Définition: Soit $G = (V, \Sigma, S, R)$ une grammaire. $G$ est régulière si les règles de réécriture respecte les restrictions suivantes:
- Les termes de gauche consistent en un seul symbole non terminal.
-
Les termes de droit consistent en soit
- un symbole terminal suivi d’un symbole non terminal
- un seul symbole terminal
- $\lambda$
Exemple
$$ \begin{align} S & \rightarrow bS & S & \rightarrow a & S & \rightarrow \lambda \end{align} $$
Remarque
À cause de ces restrictions, une grammaire régulière permet de générer les symboles de gauche à droite.
Après $k$ applications de règles de production qui ne sont pas des $\lambda$-règles le mot généré est de la forme
$$a_1a_2...a_kA$$
où $a_i \in \Sigma$ et $A \in V$
Théorème
Soit $G$ une grammaire.
$$L(G) \text{ est régulier } \Longleftrightarrow G \text{ est régulière }$$
Grammaire hors contexte
Définition: Soit $G = (V, \Sigma, S, R)$ une grammaire. $G$ est hors contexte si les règles de réécriture respecte les restrictions suivantes:
- Les termes de gauche consistent en un seul symbole non terminal.
Exemple
$$ \begin{align} S & \rightarrow SS & S & \rightarrow aSb \\ S & \rightarrow \lambda \end{align} $$
Grammaire hors contexte
Ce type de grammaire est le plus utilisé en informatique.
Les grammaires BNF (Backus-Naur Form), utilisées pour définir la syntaxe des langages de programmation, sont des grammaires équivalentes aux grammaires non contextuelles.
grammaires BNF
<expr> ::= <term> "+" <expr>
| <term>
<term> ::= <factor> "*" <term>
| <factor>
<factor> ::= "(" <expr> ")"
| <const>
<const> ::= integer
Remarques
Les grammaires non contextuelles génèrent des chaînes par dérivation tout comme les grammaires régulières.
Mais dans le cas des grammaires non contextuelles, au cours du processus de dérivation, la possibilité peut s’offrir à nous de choisir parmi plusieurs non terminaux à remplacer.
Exemple
$$ \begin{align} S \to & zMNz \\ M \to & aMa \mid z \\ N \to & bNb \mid z \end{align} $$
$$ S \overset{*}{\Rightarrow} zazabzbz$$
Dérivation à gauche
Une dérivation à gauche s’effectue en remplaçant toujours, à chaque étape du processus de dérivation, le non terminal le plus à gauche.
Dérivation à droite
Une dérivation à droite s’effectue en remplaçant toujours, à chaque étape du processus de dérivation, le non terminal le plus à droite.
Arbre de dérivation
La racine de l’arbre de dérivation est l’axiome de la grammaire.
Les non terminaux forment les nœuds internes et les terminaux forment les feuilles.
Exemple
$$ \begin{align} S \to & S + S \\ S \to & S * S \\ S \to & ( S ) \\ S \to & S - S \\ S \to & S \ / \ S \\ S \to & a \end{align} $$
$$ S \overset{*}{\Rightarrow} a+a*a$$
grammaire ambiguë
Une grammaire est dite ambiguë si elle permet plus d’un arbre de dérivation pour une séquence terminale donnée.
Langage hors contexte
Définition: Un langage est dit hors contexte (ou non contextuelle) s’il existe une grammaire hors contexte qui le génère.
Forme normale de Chomsky
Définition: Soit $G = (V, \Sigma, S, R)$ une grammaire. $G$ est dans la forme normale de Chomsky si les règles de réécriture sont de la forme:
- $A \to BC$ pour $A, B, C \in V$ et $B \ne S$ et $C \ne S$
- $A \to a$ pour $A \in V$, $a \in \Sigma$.
- $S \to \lambda$ pour le symbole de départ $S$.
Noam Chomsky

Noam Chomsky est un linguiste et philosophe américain. Professeur émérite de linguistique au Massachusetts Institute of Technology où il a enseigné toute sa carrière, il a fondé la linguistique générative. Il s'est fait connaître du grand public, à la fois dans son pays et à l'étranger, par son parcours d'intellectuel engagé de sensibilité anarchiste.
Théorème
Tout langage hors contexte est généré par une grammaire dans la forme normale de Chomsky.
Transformation
Il est possible de transformer un grammaire hors context en grammaire dans la forme normale de Chomsky.
- Ajouter une variable $S_0$
- Remplacer les règles-$\lambda$
- Remplacer les règles unitaires
- Ajouter des variables pour les règles trop longue
Automate à pile
Introduction
Pour augmenter la puissance des automates finis, on leur donne de la mémoire en leur ajoutant une pile.
Alphabet de la pile
La pile de l’automate à pile a son propre alphabet qui peut être différent de l’alphabet d’entrée.
Automate à pile
Définition: Un automate à pile consiste en un sixtuplet de la forme $(S, \Sigma, \Gamma, \delta, \iota, F)$ où
- $S$ est un ensemble fini d’états.
- $\Sigma$ est l’alphabet d’entrée (alphabet du ruban).
- $\Gamma$ est l’alphabet de la pile.
- $\delta : S \times \Sigma_\lambda \times \Gamma_\lambda \to \mathcal P(S \times \Gamma_\lambda)$ est la fonction de transition.
- $\iota \in S$ est l’état initial.
- $F \subseteq S$ est l’ensemble des états finaux (ou accepteurs ou acceptants).
Opérations
Les opérations que peut effectuer un automate à pile sont les suivantes:
- Lire un symbole (et avancer la tête de lecture)
- Dépiler un symbole
- Empiler un symbole
- Changer d’état
Le choix d’opération dépend de l’état courant, du symbole lu sur le ruban d’entrée et du symbole apparaissant sur le dessus de la pile.
Transition
On décrit une transtion de l'automate à pile par
$$p, x, y \to q, z$$
- $p$ l'état courant
- $x$ est le symbole à l’entrée
- $y$ est le symbole dépilé
- $q$ est le nouvel état
- $z$ est le symbole empilé
Remarques
- Le $y$ est dépilé avant que le $z$ ne soit empilé.
- Si aucun symbole n’est lu, on met un $\lambda$ à la place du $x$.
- Si aucun symbole n’est dépilé, on met un $\lambda$ à la place du $y$.
- Si aucun symbole n’est empilé, on met un $\lambda$ à la place du $z$.
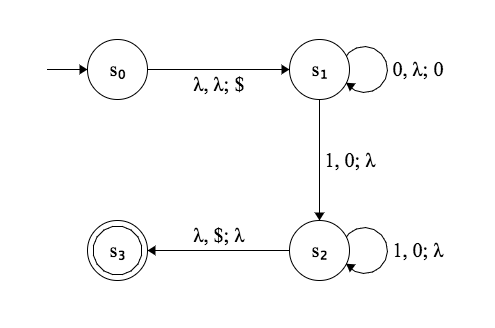
Exemple
Soit l'automate à pile suivant $M = (S, \Sigma, \Gamma, \delta, \iota, F)$ tel que
$$ \begin{align} S = & \{s_1, s_2, s_3, s_4 \} \\ \Sigma = & \{0, 1 \} \\ \Gamma = & \{0, $ \} \\ \iota = & s_1 \\ F = & \{s_1, s_4 \} \end{align} $$
$$ \begin{align} \delta = \{ & (s_1, \lambda, \lambda \to s_2, $), (s_2, 0, \lambda \to s_2, 0), \\ & (s_2, 1, 0 \to s_3, \lambda), (s_3, 1, 0 \to s_3, \lambda), \\ & (s_3, \lambda, $ \to s_4, \lambda) \} \end{align} $$
Diagrame de transitions
Les diagrammes de transitions des automates à pile sont comme ceux des automates finis sauf que l’étiquette d’un arc est plus complexe.
Ces étiquettes ont la forme $x, y \to z$, où
- $x$ est le symbole lu sur le ruban,
- $y$ est le symbole dépilé et
- $z$ est le symbole empilé.
Exemple
Exercice
Donner un automate à pile qui accepte $L= \{ ww^R \mid w \in \{0,1\}^* \}$.
Exercice
Donner un automate à pile qui accepte $L= \{a^ib^jc^k \mid i,j,k ≥ 0 \text{ et } i = j \text{ ou } i = k \}$.
Théorème
$L$ est un language hors context si et seulement si un automate à pile accepte $L$.