IFT-2002
Informatique Théorique
H14 - cours 3
Julien Marcil - julien.marcil@ift.ulaval.ca
Cours précédents
Langage régulier
Définition: Un langage est dit régulier s’il existe un automate fini déterministe qui le reconnaît.
Une façon de montrer qu’un langage est régulier est de construire un automate qui reconnaît ce langage.
Automate fini déterministe
Définition: Un automate fini déterministe consiste en un quintuple de la forme $(S, \Sigma, \delta, \iota, F)$ où
- $S$ est un ensemble fini d’états.
- $\Sigma$ est l’alphabet.
- $\delta : S \times \Sigma \to S$ est la fonction de transition.
- $\iota \in S$ est l’état initial.
- $F \subseteq S$ est l’ensemble des états finaux (ou accepteurs ou acceptants).
Opérations
Soit les languages $A$ et $B$. Nous définissons les opérations suivantes:
- Union : $A \cup B = \{ x \mid x \in A \ \text{ou} \ x \in B\}$
- Concaténation : $A \circ B = \{ xy \mid x \in A, \ y \in B\}$
- Étoile : $A^* = \{ x_1x_2\dots x_k \mid k \ge 0, \ x_i \in A \}$
Aujourd'hui
- Automates finis non déterministes
- Expression Régulière
- TP 1
Automates finis non
déterministes
Automate fini non déterministe
Définition: Un automate fini non déterministe consiste en un quintuple de la forme $(S, \Sigma, \delta, \iota, F)$ où
- $S$ est un ensemble fini d’états.
- $\Sigma$ est l’alphabet.
- $\delta : S \times \Sigma \to \mathcal P(S)$ est la fonction de transition.
- $\iota \in S$ est l’état initial.
- $F \subseteq S$ est l’ensemble des états finaux (ou accepteurs ou acceptants).
$M$ accepte la la séquence $x$
Définition: L’automate fini non déterministe $M = (S, \Sigma, \delta, \iota, F)$ accepte (ou reconnaît) la séquence $x = x_1x_2x_3\dots x_n$ (où $s_i \in \Sigma$) si et seulement si il existe une séquence d’états $s_0, s_1, s_2, \dots, s_n$ (où $s_i \in S$) tels que $$\iota = s_0$$ et $$\forall_{j=1,\dots,n} \ s_j \in \delta(s_{j-1}, x_j)$$ et $$ s_n \in F $$
Dans le cas contraire, on dit que l’automate rejette la séquence.
Théorème
Pour tout automate fini non déterministe, il existe un automate fini déterministe qui accepte exactement le même langage.
Exemple
Constuire de l’automate fini déterministe équivalent au diagramme de transisition suivant
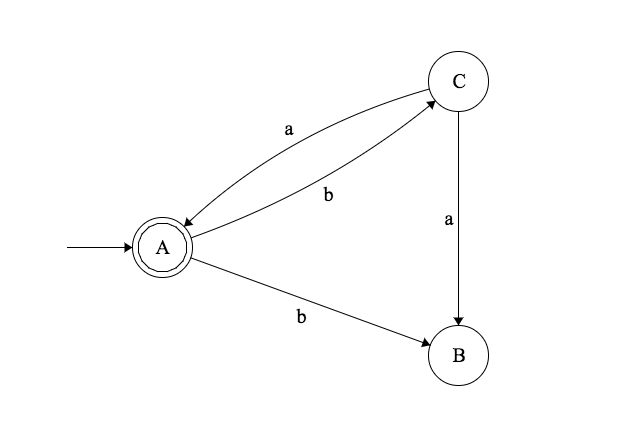
Remarques
On n’augmente donc pas la puissance des automates finis en permettant le non déterminisme.
Par conséquent, on peut dire qu’un langage est régulier si il est reconnu par un automate fini non déterministe.
Les automates finis non déterministe ont une représentation plus simple.
transition sur $\lambda$
Supposont qu'il soit aussi possible de faire des transitions sur $\lambda$. Par exemple:
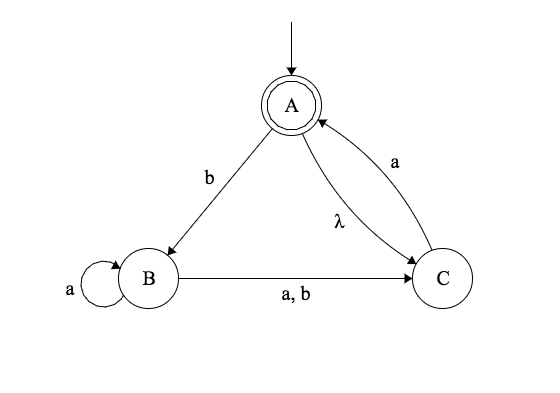
Exemple
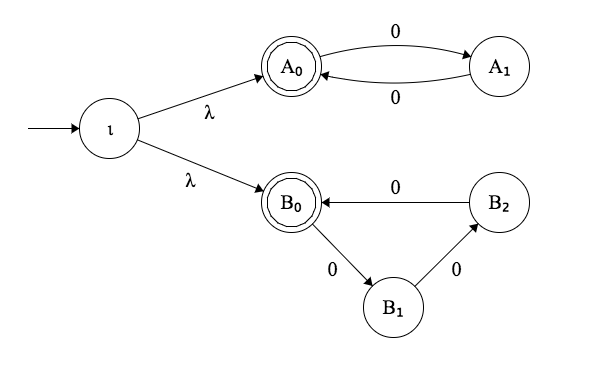
Automate fini non déterministe (avec transition sur $\lambda$)
Définition: Un automate fini non déterministe consiste en un quintuple de la forme $(S, \Sigma, \delta, \iota, F)$ où
- $S$ est un ensemble fini d’états.
- $\Sigma$ est l’alphabet.
- $\delta : S \times \Sigma_\lambda \to \mathcal P(S)$ est la fonction de transition.
- $\iota \in S$ est l’état initial.
- $F \subseteq S$ est l’ensemble des états finaux (ou accepteurs ou acceptants).
où $\Sigma_\lambda = \Sigma \cup \{\lambda\}$
Théorème
L'ensemble des languages réguliers est fermé sur les opérations: Union, Concaténation et Étoile.
Expression régulière
Observation
Soit $L = \{a^mba^n \mid m \in \mathbb N^+, n \in \mathbb N\}$. Il est possible de décomposer $L$ en utilisant les opérations: Union, Concaténation et Étoile.
$$ L = \{a\} \circ \{a\}^* \circ \{b\} \circ \{a\}^* $$
En simplifiant, il est possible d'écrire
$$aa^*ba^*$$
Expression régulière
Définition: $R$ est une expression régulière si $R$ est:
- $a$, pour tout $a \in \Sigma$
- $\lambda$
- $\emptyset$
- $(R_1)$, pour une expression régulière $R_1$
- $R_1 \cup R_2$, pour des expressions régulières $R_1$ et $R_2$
- $R_1 \circ R_2$, pour des expressions régulières $R_1$ et $R_2$
- $R_1^*$, pour une expression régulière $R_1$
Note: Cette dénition est de nature récursive.
Observation
L'opération de concaténation est associative. Pour tous les langages $L_1$, $L_2$, $L_3$:
$$ L_1 \circ (L2 \circ L3) = (L1 \circ L2) \circ L3 $$
Par conséquent si $r_1$, $r_2$, $r_3$ sont des expressions régulières alors les expressions régulières $r_1 \circ (r_2 \circ r_3)$ et $(r_1 \circ r_2) \circ r_3$ représentent le même langage.
Notation
Pour alléger la notation, on écrira $r_1r_2$ plutôt que $r_1 \circ r_2$. Donc
$$ \begin{align} r_1r_2r_3 = & r_1 \circ r_2 \circ r_3 \\ & r_1 \circ (r_2 \circ r_3) \\ & (r_1 \circ r_2) \circ r_3 \\ \end{align} $$
Observation
L'opération d'union est associative. Pour tous les langages $L_1$, $L_2$, $L_3$:
$$ L_1 \cup (L2 \cup L3) = (L1 \cup L2) \cup L3 $$
Par conséquent si $r_1$, $r_2$, $r_3$ sont des expressions régulières alors les expressions régulières $r_1 \cup (r_2 \cup r_3)$ et $(r_1 \cup r_2) \cup r_3$ représentent le même langage:
$$r_1 \cup r_2 \cup r_3$$
Règles de priorité
- Les parentèses sont prioritaires sur toutes les autres opérations.
- L'étoile $*$ est prioritaire sur la concaténation et l'union. C'est à dire que $$ \begin{align} r_1 \cup r_2^∗ & = r_1 \cup (r_2^∗) \\ r_1 \circ r_2^∗ & = r_1 \circ (r_2^*) \end{align} $$
- La concaténation est prioritaire sur l'union. C'est à dire que $$ \begin{align} r_1 \cup r_2 \circ r_3 & = r_1 \cup (r_2 \circ r_3) \\ r_1 \circ r_2 \cup r_3 & = (r_1 \circ r_2) \cup r_3 \end{align} $$
Langage repésenté par $R$
Définition: Soit une expression régulière $R$ et un alphabet $\Sigma$. Le langage repésenté par $R$ noté $L(R)$, est défini par les propostions récursive suivantes:
- Pour tout $a \in \Sigma$, si $R=a$ alors $L(R) = \{a\}$
- Si $R=\lambda$ alors $L(R) = \{\lambda\}$
- Si $R=\emptyset$ alors $L(R) = \{\}$
- Pour des expressions régulières $R_1$ et $R_2$, si $R = R_1 \cup R_2$, alors $L(R) = L(R_1) \cup L(R_2)$
- Pour des expressions régulières $R_1$ et $R_2$, si $R = R_1 \circ R_2$, alors $L(R) = L(R_1) \circ L(R_2)$
- Pour une expression régulière $R_1$, si $R = R_1^*$, alors $L(R) = L(R_1)^*$
Exemples
| $(ab)^*$ | représente | $\{\lambda, ab, abab, \dots \}$ |
| $ab^*$ | représente | $\{a, ab, abb, abbb, \dots \}$ |
| $a \cup bc$ | représente | $\{a, bc\}$ |
| $(a \cup b)c$ | représente | $\{ac, bc\}$ |
| $ab \cup bc$ | représente | $\{ab, bc\}$ |
| $a(b \cup b)c$ | représente | $\{abc\}$ |
Exemples
| $(a \cup \lambda)b^*$ | représente | $\{ab^n~\text{ou}~b^n \mid n \in \mathbb N \}$ |
| $(a \cup \lambda)(b \cup \lambda)$ | représente | $\{\lambda, a, b, ab\}$ |
| $a^* \emptyset$ | représente | $\{\}$ |
| $\emptyset^*$ | représente | $\{\lambda\}$ |
Théorème
Soit un alphabet $\Sigma$. Les langages réguliers sur $\Sigma$ sont précisément les langages représentables par les expressions régulières sur $\Sigma$.
Démonstration
La démonstration se divise en deux parties:
- Montrer que tout langage représentable par une expression régulière est régulier.
- Montrer que tout langage régulier est représentable par une expression régulière.
Partie 1
On voit qu’une expression régulière représente toujours un langage régulier, puisque
- les expressions régulières élémentaires représentent des langages réguliers
- et que la combinaison d’expressions régulières représentant des langages réguliers est une expression régulière représentant un langage régulier.
Exercice
Convertir ces expressions régulières en automates fini non déterministe:
- $(ab \cup a)^*$
- $(a \cup b)^*aba$
Automate fini non déterministe généralisé
Remplaçons les transition par des expressions régulières:
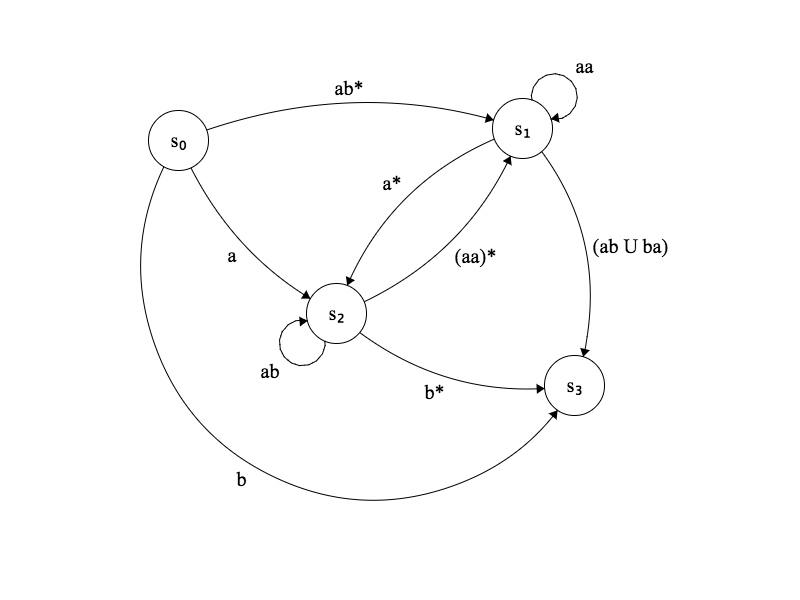
Automate fini non déterministe généralisé
Définition: Un automate fini non déterministe consiste en un quintuple de la forme $(S, \Sigma, \delta, s_{init}, s_{accepte})$ où
- $S$ est un ensemble fini d’états.
- $\Sigma$ est l’alphabet.
- $\delta : (S -\{ s_{accepte} \}) \times (S -\{ s_{init} \}) \to R$ où $R$ est une expression régulière, est la fonction de transition.
- $s_{init} \in S$ est l’état initial.
- $s_{accepte} \in S$ est l'état accepteur.
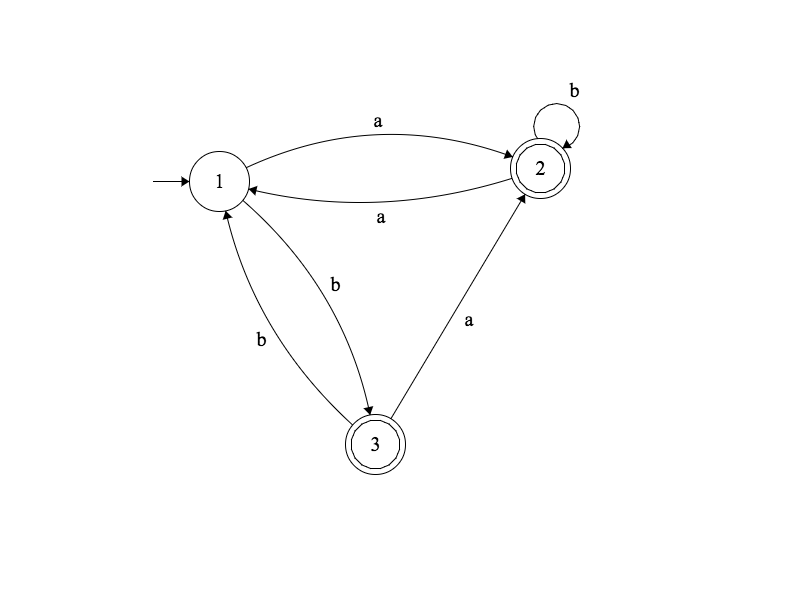
Exercice
Convertir cet automate en expression régulière
Regex
Regex
Une expression régulière (Regex) est une suite de caractères typographiques (qu’on appelle plus simplement « motif » ou « pattern » dans sa forme anglaise) décrivant une chaîne de caractères dans le but de la trouver dans un bloc de texte pour lui appliquer un traitement automatisé, comme un ajout, son remplacement ou sa suppression.
Regex
| abc | la chaîne de charactères: abc |
| abc|cba | la chaîne de charactères: abc ou cba |
| [abc] | un seul charactère: a, b ou c |
| [^abc] | n'importe quel charactère sauf a, b ou c |
| [a-z] | n'importe quel charactère entre a et z |
| [a-zA-Z] | n'importe quel charactère entre a et z ou A et Z |
| . | n'importe quel charactère |
Regex
| a? | zero ou un charactère a |
| a* | zero ou plus charactères a |
| a+ | un ou plus charactères a |
| a{3} | exactement 3 charactères a |
| a{3,} | trois ou plus charactères a |
| a{3,6} | entre 3 et 6 charactères a |
Regex
| ^ | le début de la ligne |
| $ | la fin de la ligne |
| POSIX | Description | ASCII | |
|---|---|---|---|
| [:alnum:] | Alphanumeric characters | [a-zA-Z0-9] | |
| [:alpha:] | Alphabetic characters | [a-zA-Z] | |
| [:blank:] | Space and tab | [ \t] | \h |
| [:digit:] | Digits | [0-9] | \d |
| [:lower:] | Lowercase letters | [a-z] | |
| [:space:] | All whitespace characters, including line breaks | [ \t\r\n\v\f] | \s |
| [:upper:] | Uppercase letters | [A-Z] | |
| [:word:] | Word characters (letters, numbers and underscores) | [A-Za-z0-9_] | \w |