IFT-2002
Informatique Théorique
H14 - cours 1
Julien Marcil - julien.marcil@ift.ulaval.ca
Objectifs
- Comprendre les fondements théoriques de l’informatique.
- Formaliser la notion de calcul automatique.
- Raisonner à propos de la puissance et des limites d’un modèle de calcul donné.
Modèles de calcul
Nous étudierons des modèles de calcul de plus en plus sophistiqués, en analysant les limites de chaque modèle.
- Automates finis et expressions régulières
- Automates à piles et grammaires hors contexte
- Machines de Turing
Pourquoi prendre le temps d’étudier des modèles non-sophistiqués?
- Parce que plus un modèle de calcul est sophistiqué et moins on peut raisonner à propos de son comportement.
- Parce que ces modèles sont utilisés en pratique… même si ça semble surprenant!
Limites des ordinateurs
En apprenant à programmer, on a souvent l’impression que toute tâche de calcul est réalisable par un programme suffisamment long et complexe. Cette intuition est fausse et certaines tâches n’admettent aucun algorithme.
Préliminaires et Révision
Théorie des ensemble
- L’ensemble vide, noté $\{\}$ ou $\emptyset$ est l ’ensemble qui ne contient aucun élément.
- L’appartenance de l’élément $a$ à l’ensemble $A$ est noté $a \in A$.
- Si $a \in A \Rightarrow a \in B$ alors l’ensemble $A$ est contenu dans l’ensemble $B$, ce que l’on note $A \subseteq B$.
- Si $A \subseteq B$ et $B \subseteq A$ alors $A$ et $B$ sont égaux, c’est-à-dire qu’ils contiennent les mêmes éléments.
Produit cartésien
Le produit cartésien des ensembles $A$ et $B$, noté $A \times B$, est l’ensemble de tous les paires d'éléments de $A$ et $B$.
$$A \times B = \{(a,b) \mid a \in A, b \in B \}$$
Exemple
\[\begin{aligned} \{a,b\}\times\{1,2,3\} = \{ &(a,1), (a,2), (a,3), \\ & (b,1), (b,2), (b,3) \} \\ \{1,2\}^2= \{ & (1,1), (1,2), (2,1), (2,2) \} \end{aligned} \]
Ensemble puissance
L’ensemble puissance de $A$, noté $\mathcal P(A)$, est l’ensemble de tous les sous-ensembles de $A$.
$$\mathcal P(A) = \{E \mid E \subseteq A\}$$
\[\begin{aligned} \mathcal P(\{0,2,4\}) = \{ &\emptyset,\{0\},\{2\},\{4\}, \\ & \{0,2\},\{2,4\},\{0,4\},\{0,2,4\}\} \end{aligned} \]
Fonction
$f: A \to B$ signifie que $f$ est une fonction de l'ensemble $A$ dans l'ensemble $B$.
Injection
Une fonction est injective si $\forall x, y \in X,\ x \ne y \Rightarrow f(x) \ne f(y)$
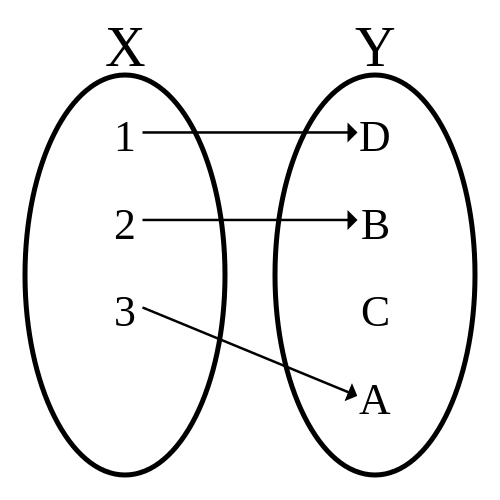
Surjection
Une fonction est surjective si $\forall y \in Y,\ \exists x \in X,\ f(x) = y$
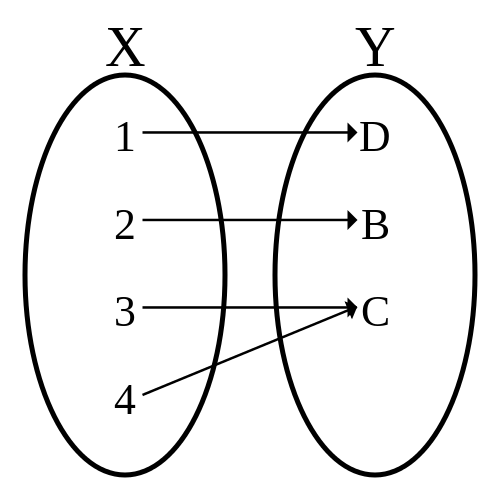
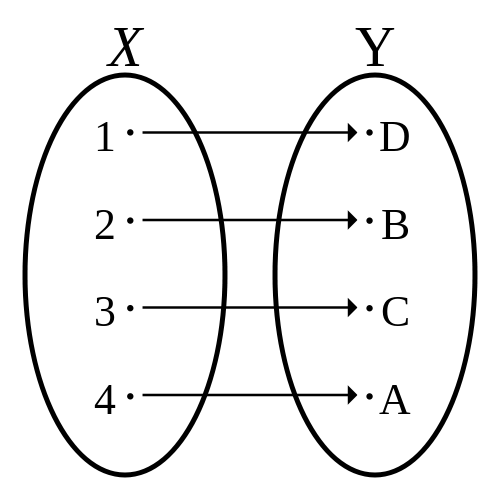
Bijection
Une fonction est bijective si elle est injective et surjective.
Cardinalité d’un ensemble
La cardinalité d’un ensemble $S$, notée $\left\vert{S}\right\vert$, est la taille de cet ensemble, la quantité d’éléments qu’il contient.
Exemple
$$ \left\vert{\{i \in \mathbb{N} \mid 0 \le i < n\}}\right\vert = n $$
Definitions
La cardinalité d’un ensemble $S_1$ est inférieure ou égale à la cardinalité d’un ensemble $S_2$ (dénoté par $\left\vert{S_1}\right\vert \le \left\vert{S_2}\right\vert$) ssi il existe une fonction injective $f: S_1 \to S_2$.
La cardinalité d ’un ensemble $S_1$ est égale à la cardinalité d’un ensemble $S_2$ (dénoté par $\left\vert{S_1}\right\vert=\left\vert{S_2}\right\vert$) ssi il existe une fonction bijective $f: S_1 \to S_2$.
La cardinalité d ’un ensemble $S_1$ est inférieure à la cardinalité d’un ensemble $S_2$ (dénoté par $\left\vert{S_1}\right\vert < \left\vert{S_2}\right\vert$) ssi $\left\vert{S_1}\right\vert \le \left\vert{S_2}\right\vert$ et $\left\vert{S_1}\right\vert \ne \left\vert{S_2}\right\vert$.
Ensembles finis et infinis
Un ensemble $S$ est dit fini ssi $\left\vert{S}\right\vert < \left\vert{\mathbb{N}}\right\vert$
Un ensemble $S$ est dit infini ssi $\left\vert{S}\right\vert \ge \left\vert{\mathbb{N}}\right\vert$
Ensembles dénombrables et non dénombrables
Un ensemble $S$ est dénombrable ssi on peut donner une méthode pour énumérer ses éléments de telle sorte que n’importe quel élément soit nommé après un nombre fini d’étapes.
Il existe donc une bijection $ f : \mathbb{N} \to S $.
Exemple
Soit $T = \{k \mid \exists_{n \in \mathbb{N}} \ k = 3n\}$
La fonction $f: \mathbb{N} \to T$, définie $f(n)=3n$, est bijective.
Donc $T$ est dénombrable, $\left\vert{T}\right\vert=\left\vert{\mathbb{N}}\right\vert$.
$\mathbb{N} \times \mathbb{N}$ est dénombrable
Énumérer les couples dont la somme des composantes est 0, ensuite 1, puis 2, ...
| Somme | |||||
|---|---|---|---|---|---|
| 0 | (0, 0) | ||||
| 1 | (1, 0) | (0, 1) | |||
| 2 | (2, 0) | (1, 1) | (0, 2) | ||
| 3 | (3, 0) | (2, 1) | (1, 2) | (0, 3) | |
| 4 | (4, 0) | (3, 1) | (2, 2) | (1, 3) | (0, 4) |
| 5 | ... | ||||
Ensembles non dénombrables
Nous avons défini ce qu’est un ensemble non dénombrable mais nous n’en avons pas encore rencontré.
Théorème
Soit un ensemble $S$ (fini ou infini).
$$ \left\vert{S}\right\vert < \left\vert{\mathcal P(S)}\right\vert $$
Démonstrations par contradiction
Dans une démonstration, quand on arrive à une contradiction, on peut conclure que la dernière hypothèse qu’on a faite était fausse.
C’est ce même raisonnement qui nous permet de faire une démonstration par contradiction : on suppose que ce qu’on veut démontrer est faux, et on démontre que ça implique une contradiction. Ce genre de démonstration est basé sur l’équivalence :
$$ (\neg p \Rightarrow \text{faux}) \Leftrightarrow p$$
Démonstration
- $\left\vert{S}\right\vert \le \left\vert{\mathcal P(S)}\right\vert$ car la fonction $g : S \to \mathcal P(S)$ définie par $g(s) = \{s\}$ est injective.
- Pour montrer que $\left\vert{S}\right\vert \ne \left\vert{\mathcal P(S)}\right\vert$ il faut prouver qu'il n’existe pas de fonction surjective de $S \to \mathcal P(S)$.
Corollaire
$$ \left\vert{\mathbb{N}}\right\vert < \left\vert{\mathcal P(\mathbb{N})}\right\vert $$
Ce corollaire montre qu’il y a des ensembles infinis de cardinalités différentes.
Chapitre 1
Automates finis et langages réguliers
Qu’est-ce qu’un calcul?
$$ \begin{align} \text{Entrée} \longrightarrow & \boxed{\text{Machine}}& \longrightarrow & \text{Sortie} \\ \mathbb{N} \longrightarrow & f : \mathbb{N} \to \mathbb{N} & \longrightarrow & \mathbb{N} \end{align} $$
Langage
Alphabet
Définition: Un alphabet est un ensemble fini non vide de symboles. Souvent dénoté par $\Sigma$.
Exemple : $\Sigma = \{a, b, c\}$.
Un caractère et un symbole sont des synonymes.
Une chaîne, une séquence, une suite de caractères ou un mot sont des synonymes.
Exemples
- Les caractères ASCII forme un alphabet de 256 lettres.
- $\{a,b,c\}$ est un alphabet.
- $\{0,1\}$ est l’alphabet binaire.
- $\mathbb{N}$ n’est pas un alphabet.
- $1100$ est un mot de l’alphabet binaire.
Concaténation
Définition: La concaténation de deux séquences $s_1$ et $s_2$ notée $s_ 1s_2$ est une séquence composée de tous les symboles de $s_1$ suivis de ceux de $s_2$.
Séquence vide
Définition: La séquence ne contenant aucun symbole, appelée séquence vide, fait partie des séquences de symboles. Elle est dénotée $\lambda$.
$$\lambda s = s\lambda= s$$
Opérateur de Kleene
Définition: Le symbole $^*$ représente l’opérateur de Kleene, qui, appliqué à un alphabet $\Sigma$, donne l'ensemble infini $\Sigma^*$ de toutes les séquences finies de symboles de cet alphabet. On dit que $\Sigma^*$ est la fermeture de l’alphabet $\Sigma$.
Note : la séquence vide $\lambda$ appartient à $\Sigma^*$ pour tout alphabet $\Sigma$.
La fermeture d’un alphabet est un ensemble infini mais dénombrable.
Exemple
Si $\Sigma = \{a,b,c\}$ alors
$$ \Sigma^* = \{\lambda, a, b, c, aa, ab, ac, \dots, aaa, aab, aac, \dots, \\ aaaa, aaab, aaac, \dots\} $$
Notation
Soient $\Sigma$ un alphabet quelconque, $s \in \Sigma^*$ et $n \in \mathbb{N}$. Alors, $$s^n = \underbrace{s \dots s}_{n~\text{fois}}$$
Exemple
\[\begin{aligned} a^4 & = aaaa \\ (mn)^2t^3 & = mnmnttt \end{aligned} \]
Exemple
L’ensemble $\{a^mba^n : m \in \mathbb{N}, n \in \mathbb{N}\}$ est l’ensemble des séquences ayant un seul $b$, précédé et suivi d’un nombre quelconque de $a$.
Le nombre de $a$ qui précède ce $b$ n’est pas nécessairement le même que celui qui suit.
$\Sigma^*$ et $\mathcal P(\Sigma)$
Il y a une certaine similarité entre $\Sigma^*$ et $\mathcal P(\Sigma)$ mais ces ensembles sont bien différents.
Exemple
Soit $\Sigma = \{a\}$. \[\begin{aligned} \mathcal P(\Sigma) & = \{ \emptyset, \{ a \} \} \\ \Sigma^* & = \{ \lambda, a, aa, aaa, \dots \} \end{aligned} \]
Longueur d’une séquence
Définition: La longueur d’une séquence finie $w$, notée $\left\vert{w}\right\vert$, est le nombre de symboles qu’elle contient.
Exemple
Soit $\Sigma = \{a, b, c\}$. \[\begin{aligned} \left\vert{a}\right\vert & = 1 \\ \left\vert{abc}\right\vert & = 3 \\ \left\vert{aaa}\right\vert & = 3 \end{aligned} \]
Langage
Définition: Un langage sur un alphabet $\Sigma$ est un sous-ensemble de l’ensemble $\Sigma^*$.
Exemple
Soit $\Sigma = \{a, b, c\}$. Les ensembles suivants sont des langages sur $\Sigma$: \[\begin{aligned} L_1 & = \{a, b, aa, abc, abbc \} \\ L_2 & = \{ \lambda, a, aa, aaa, \dots \} \end{aligned} \]
Remarques
- Un langage peut être fini ou infini.
- Un langage peut contenir la séquence vide ou ne pas la contenir.
- Les séquences d’un langage sont toujours finies (par définition de $\Sigma^*$).
Remarques
L’ensemble de tous les langages sur un alphabet $\Sigma$ est $\mathcal P(\Sigma^*)$.
Comme $\Sigma^*$ est infini et que $$\left\vert{\Sigma^*}\right\vert < \left\vert{\mathcal P(\Sigma^*)}\right\vert$$ on voit que l’ensemble des langages sur un alphabet donné est non dénombrable.
Pourquoi s’intéresser aux langages
Considérons des machines $M$ dont les entrées sont un mot d’un alphabet $\Sigma$ et dont la sortie est toujours $0~\text{ou}~1$.
$$ \begin{align} \text{Entrée} \longrightarrow & \boxed{M}& \longrightarrow & \text{Sortie} \\ \Sigma^* \longrightarrow & f : \Sigma^* \to \{0,1\} & \longrightarrow & \{0,1\} \end{align} $$
On peut aussi dire que la machine accepte ou rejette son entrée.
Langage d'une machine
Définition: L’ensemble des mots acceptés par la machine $M$ est le langage de $M$ que l’on notera $L(M)$
$$ L(M) \in \mathcal P(\Sigma^*) $$
Théorème
Il existe une fonction que votre langage de programmation favori ne peut calculer.
Démonstration
- On va montrer d’une part que le nombre de programmes est infini et dénombrable.
- Ensuite que le nombre de fonctions $f : \mathbb N \to \{0,1\}$ est non-dénombrable.
Conclusion
L’ensemble des programmes que l’on peut écrire est dénombrable. Donc, il existe un nombre infini non-dénombrable de fonctions pour lesquelles il n’existe aucun programme capable de les calculer.
Automates finis déterministes
Automates finis déterministes
- Premier modèle de calcul que nous allons étudier.
- Simple (voire primitif)
- Facile à comprendre et à étudier
- Permet de modéliser un grand nombre de systèmes.
Diagrammes de transitions
Un diagramme de transitions est une collection finie d’états (cercles) et de transitions (arcs orientés) tel que:
- Chaque état peut être étiqueté.
- Il y a un seul état initial (une petite flèche le pointe).
- Les cercles doubles sont les états finaux (accepteurs). Il peut y en avoir plusieurs.
- Chaque transition relie deux états, pas obligatoirement différents.
- Chaque transition est étiquetée par un symbole d’un alphabet associé au diagramme.
Exemple
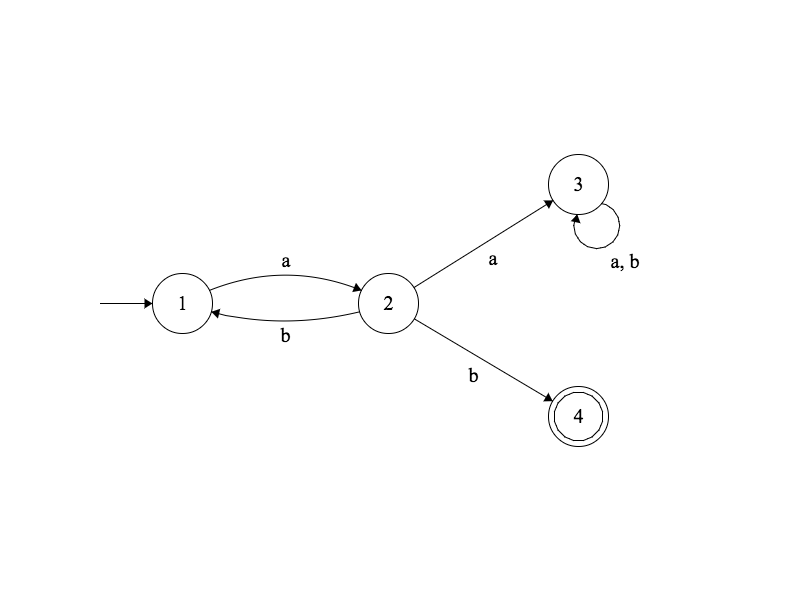
Table de transitions
Une table de transitions associée à un diagramme de transitions est une matrice à deux dimensions telle que:
- La matrice a une ligne pour chaque état du diagramme.
- Elle a une colonne pour chaque symbole utilisé comme étiquette d’un arc du diagramme.
- L’entrée de la $n^\text{ième}$ ligne et de la $m^\text{ième}$ colonne est l’état atteint dans le diagramme de transitions en quittant l’état $n$ par l’arc dont l’étiquette est celle de la colonne $m$. Si un tel état n’existe pas, l’entrée contient le mot $\text{ERREUR}$.
- On ajoute une colonne indicée par le caractère spécial de fin de séquence $\text{FIN}$. Une entrée de cette colonne est le mot $\text{ACCEPTE}$ si l’état(ligne) est final ou $\text{ERREUR}$ sinon.
Exemple
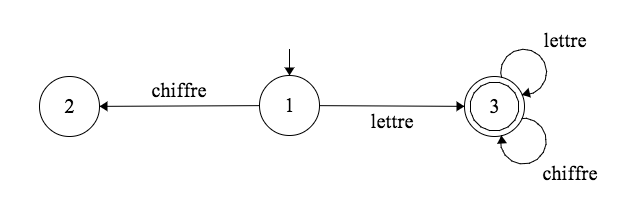
| lettre | chiffre | FIN | |
|---|---|---|---|
| 1 | 3 | 2 | $\text{ERREUR}$ |
| 2 | $\text{ERREUR}$ | $\text{ERREUR}$ | $\text{ERREUR}$ |
| 3 | 3 | 3 | $\text{ACCEPTE}$ |
Diagramme complètement défini
Définition: Un diagramme de transitions avec un alphabet $\Sigma$ est dit complètement défini si, pour chaque symbole $s \in \Sigma$ et chaque état $e$, il y a au moins une transition étiquetée $s$ qui quitte $e$.
Exemple
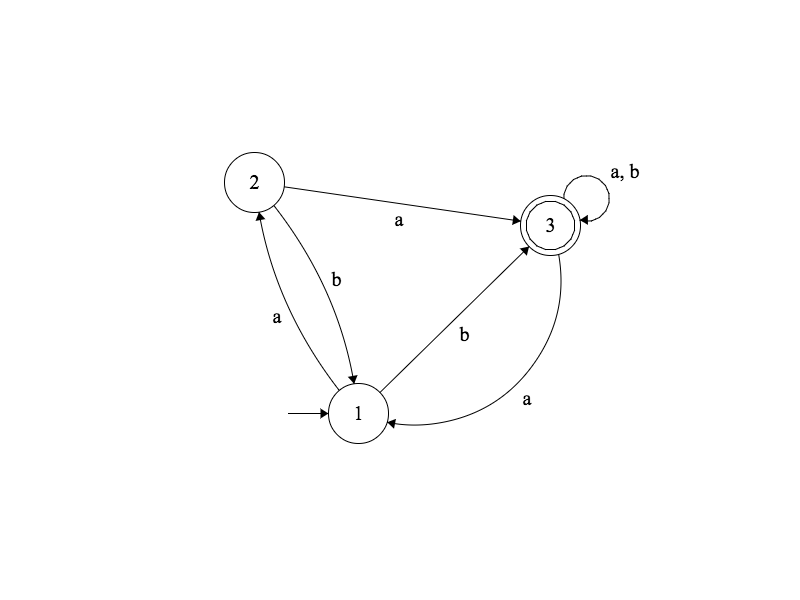
Diagramme non ambigu
Définition: Un diagramme de transitions avec un alphabet $\Sigma$ est dit non ambigu si, pour chaque état et chaque symbole $s \in S$, il existe au plus une transition quittant $e$ et étiquetée $s$.
Exemple
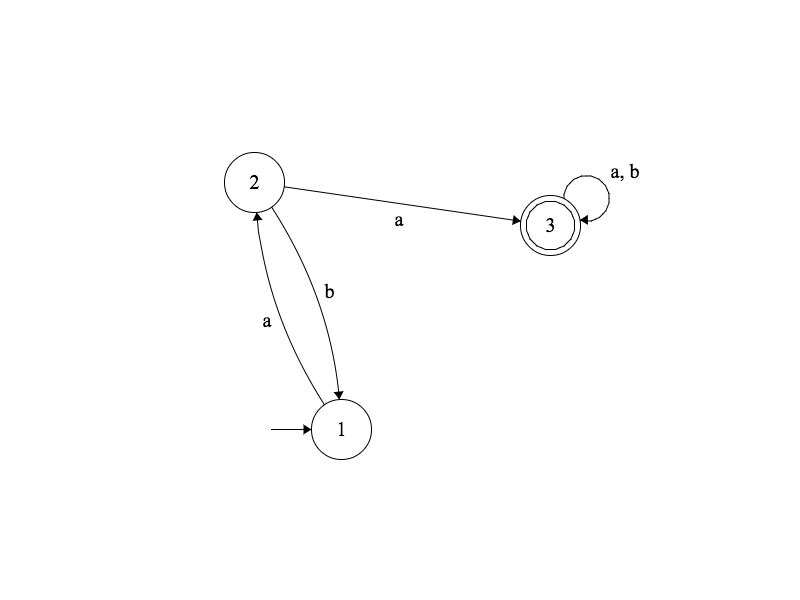
Diagramme déterministe
Définition: Un diagramme de transitions avec un alphabet $\Sigma$ est dit déterministe si il est complètement défini et non ambigu.
Exemple
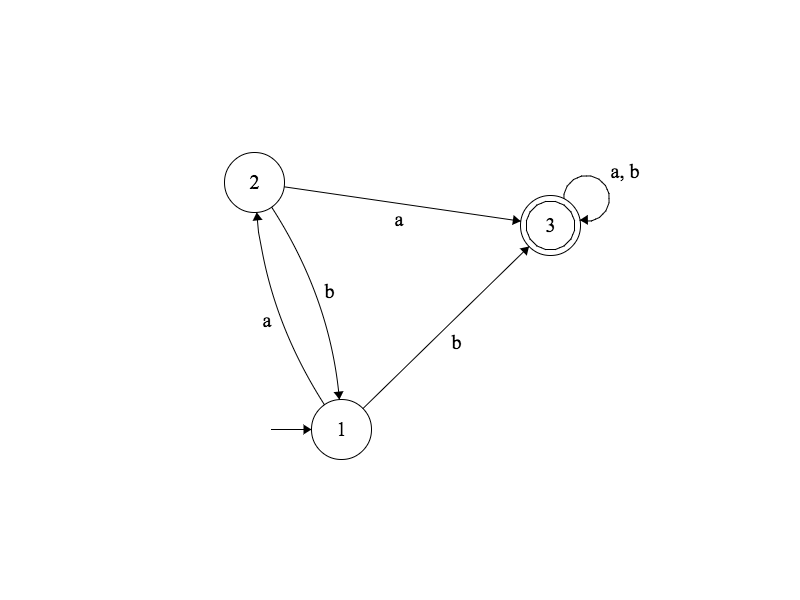
Automate fini déterministe
Définition: Un automate fini déterministe consiste en un quintuple de la forme $(S, \Sigma, \delta, \iota, F)$ où
- $S$ est un ensemble fini d’états.
- $\Sigma$ est l’alphabet.
- $\delta : S \times \Sigma \to S$ est la fonction de transition.
- $\iota \in S$ est l’état initial.
- $F \subseteq S$ est l’ensemble des états finaux (ou accepteurs ou acceptants).
Exemple
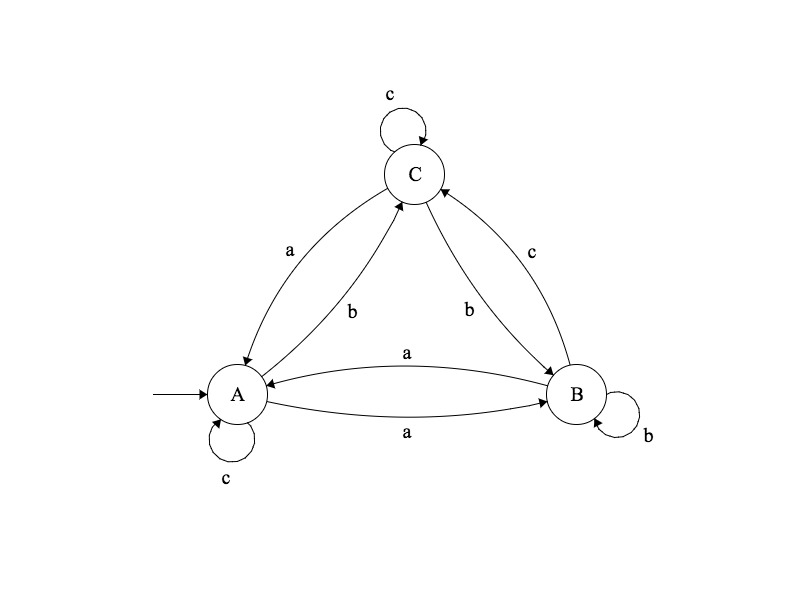
$$ M =(\{A, B, C\}, \{a, b, c\}, \delta, A, \{A, B\}) $$
| $\delta(A, a) = B$ | $\delta(A, b) = C$ | $\delta(A, c) = A$ |
| $\delta(B, a) = A$ | $\delta(B, b) = B$ | $\delta(B, c) = C$ |
| $\delta(C, a) = A$ | $\delta(C, b) = B$ | $\delta(C, c) = C$ |
- un ensemble d’états $\{A, B, C\}$
- un alphabet $\{a, b, c\}$
- une fonction de transtion $\delta$
- un état initial $A$
- un ensemble d’états finaux $\{A, B\}$
Diagramme de transitions
Exercice
Donner le diagramme de transitions de l’automate suivant: $M = (\{0, 1, 2, 3\}, \{f, g, h\}, \delta, 0, \{2\})$
tel que
| $\delta(0, f) = 3$ | $\delta(0, g) = 1$ | $\delta(0, h) = 1$ |
| $\delta(1, f) = 1$ | $\delta(1, g) = 2$ | $\delta(1, h) = 3$ |
| $\delta(2, f) = 0$ | $\delta(2, g) = 3$ | $\delta(2, h) = 3$ |
| $\delta(3, f) = 3$ | $\delta(3, g) = 3$ | $\delta(3, h) = 3$ |
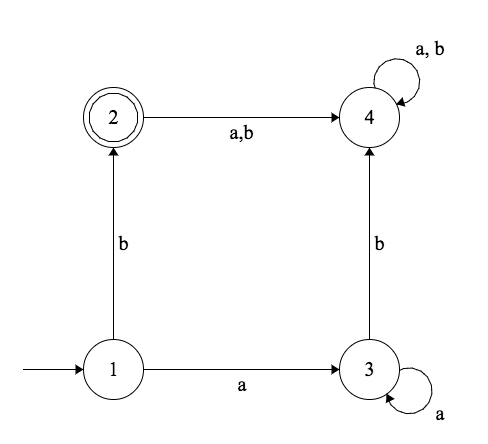
Exercice
Soit $\Sigma = \{a, b\}$. Donner l’automate $M$ correspondant au diagramme de transition ci-dessous.
Caractéristiques
Un automate fini déterministe possède les caractéristiques suivantes:
- Pour chaque couple $(p, x) \in S \times \Sigma$, il existe un et un seul $q$ tel que $\sigma(p, x) = q$. (définition d’une fonction)
- À tout automate fini déterministe correspond un diagramme de transitions déterministe (parce que $\delta$ est totale et non ambiguë).
- Le qualificatif fini signifie que l’automate possède un nombre fini d’états, que son alphabet et que son ensemble de transitions sont finis.
Machine à ruban
On peut voir un automate comme une machine avec un ruban contenant une séquence de symboles à analyser, une tête de lecture et un mécanisme de contrôle qui peut changer d’état.

Machine à ruban
L’automate accepte la séquence d’entrée si et seulement si la transition effectuée lors de la lecture du dernier symbole l’amène dans un état final (accepteur).
$M$ accepte la la séquence $x$
Définition: L’automate fini déterministe $M = (S, \Sigma, \delta, \iota, F)$ accepte (ou reconnaît) la séquence $x = x_1x_2x_3\dots x_n$ (où $s_i \in \Sigma$) si et seulement si il y a une séquence d’états $s_0, s_1, s_2, \dots, s_n$ (où $s_i \in S$) tels que $$\iota = s_0$$ et $$\forall_{j=1,\dots,n} \ \delta(s_{j-1}, x_j) = s_j$$ et $$ s_n \in F $$
Dans le cas contraire, on dit que l’automate rejette la séquence.
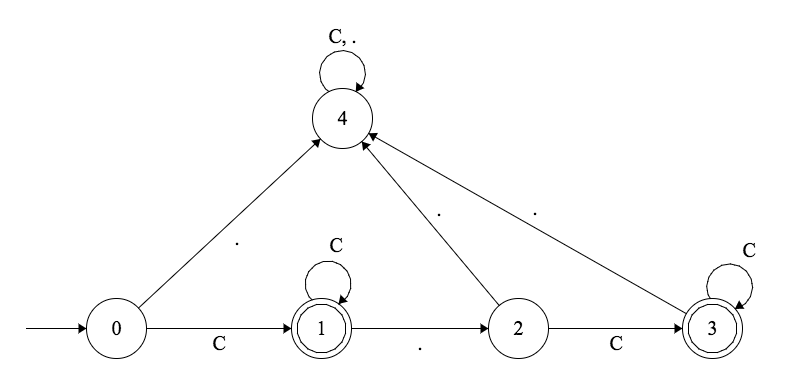
Exemple
Soit M l’automate déterministe décrit par le diagramme de transitions suivant. Son alphabet est $\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, .\}$. Le symbole $C$ représente l’ensemble des chiffres: $C = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}$
Séquence vide
La séquence vide et elle est acceptée par $M = (S, \Sigma, \delta, \iota, F)$ si l’état initial est aussi un état final ($\iota \in F$). Aucune transition n’est faite.